Streuungswerte
Hier gibt es ein schönes Video zum Thema!
Während die Mittelwerte Maße der zentralen Tendenz sind, geben die Streuungswerte Auskunft über die Homogenität bzw. Heterogenität von Variablenwerten.
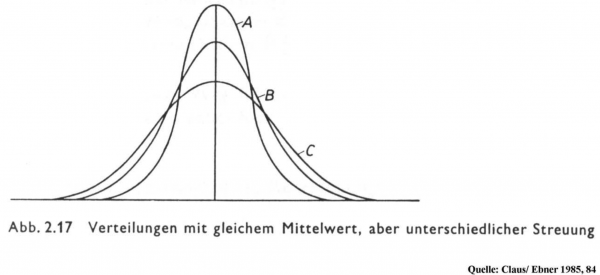
Die wichtigsten Maßzahlen zur Bestimmung der Streuung:
1. Range (total range, Spannweite, Variationsweite)
Der Range ist die Differenz zwischen dem größten und dem kleinsten Meßwert:
R = xmax – xmin
Diese Maßzahl kann nur bei metrischen Daten verwendet werden und informiert eher über die Grenzen der Streuung, als über die Streuung der Verteilung.
2. (mittlerer) Quartilsabstand (interquartile range, range deviation)
Ein Quartil (Q) ist der Schnittpunkt zwischen Vierteln und trennt die oberen (Q3) bzw. unteren 25 Prozent (Q1) von den mittleren 50 Prozent der Fälle. Das zweite Quartil ist identisch mit dem Median.
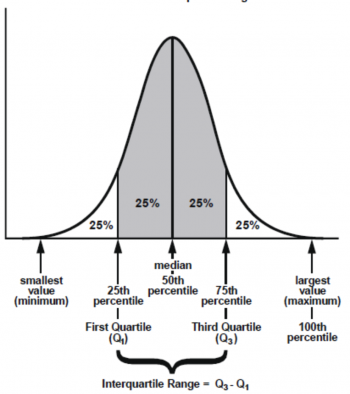
Quartilabstand = Q3 – Q1
mittlere Quartilabstand = QA = (Q3 – Q1)/2
Der Quartilabstand ist sinnvoll immer dann zu bestimmen, wenn die mittleren 50 Prozent der Fälle von besonderem Interesse sind, was meistens bei extrem schiefen Verteilungen oder solchen mit sehr extremen Werten der Fall ist.
Analog dazu lassen sich die Werte in beliebig große Unterteilungen (Quantile) einteilen. Erfolgt die Einteilung in zehn Abschnitte, spricht man von ‚Dezil'(D), sind es hundert, von ‚Centil'(C).
Für eine sinnvolle Interpretation müssen die Variablen mindestens intervallskalierte Werte aufweisen.
3. Durchschnittliche Abweichung (average deviation)
Die durchschnittliche Abweichung (AD) ist der Durchschnitt der absoluten Abweichungen aller Meßwerte von ihrem arithmetischen Mittel. Die Richtung der Abweichung bleibt bei dieser Maßzahl unberücksichtigt (Entfernen aller Vorzeichen), es werden die absoluten Werte der gemessenen Abweichung verwendet.
Arithmetisches Mittel: 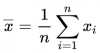
Durchschnittliche Abweichung: 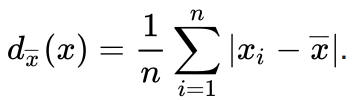
Dieses anschauliche Streuungsmaß hat (leider) in letzter Zeit an Bedeutung zu Gunsten der folgenden Maße verloren.
4. Standardabweichung und Varianz
Das gängiste Streuungsmaß ist die Standardabweichung (s), die durch Ziehen der Quadratwurzel der Varianz (s2) bestimmt wird:
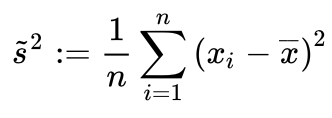
Die Varianz ist also die durch die Anzahl der Fälle dividierte Summe der quadrierte Abweichung aller Meßwerte von ihrem arithmetischen Mittel. Dementsprechend wird zunächst zu jedem Meßwert der Abstand zum arithmetischen Mittel bestimmt und quadriert. Alle diese Werte werden addiert und durch die Anzahl der Fälle geteilt.
Durch das Quadrieren der Mittelwertabweichungen wird erreicht, dass sich die Abweichungen in der Summe nicht ausgleichen. Um daraus eine lineare Maßzahl zu erhalten, wird aus der Varianz die Quadratwurzel gezogen und man erhält die Standardabweichung.
Die Standardabweichung (s) wie folgt definiert:
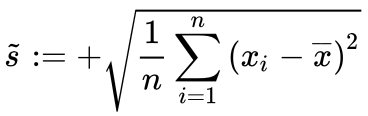
Grundsätzlich sind diese beiden Streuungsmaße gleichwertig. Für die descriptive Statistik ist die Standardabweichung oft leichter handhabbar, da die Einheit dieses Maßes nicht quadriert ist.
Beispiel:
| Varianz | s2 = 49 min2 |
| Standardabweichung | s = 7 min |
Diese Maßzahlen setzen metrische Daten vorraus und berücksichtigen alle Fälle der Verteilung. Aus diesem Grund werden sie für weiterführende Berechnungen häufig eingesetzt.