Grundbegriffe
Datenmatrix
Die Anordnung von Daten nach einem Tabellen-Schema führt zur Bildung einer Datenmatrix.
Die Zeilen repäsentieren die Untersuchungseinheiten (UEx), die Spalten bilden die Variablen (Vu) ab. Der Zelleneintrag (Wx u) ist der Wert einer Variable bezogen auf eine Untersuchungseinheit.
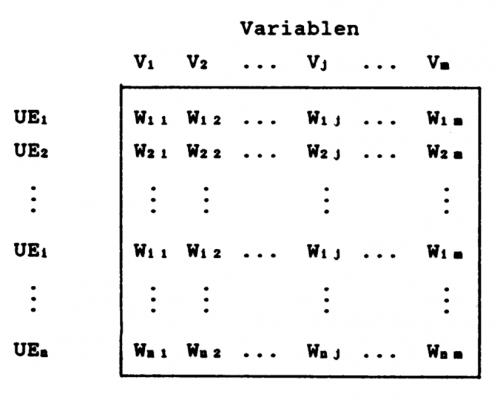
aus: Helmut Thome, Grundkurs Statistik für Historiker. Teil I: Deskriptive Statistik, HSR-TRANS 7 (2001), Version 20-12-2001,
https://www.ssoar.info/ssoar/bitstream/handle/document/28594/ssoar-hsrsupp-1989-no_2-thome-grundkurs_statistik_fur_historiker.pdf?sequence=1&isAllowed=y&lnkname=ssoar-hsrsupp-1989-no_2-thome-grundkurs_statistik_fur_historiker.pdf
Untersuchungseinheit
Merkmalsträger, Objekte, Fall
- z.B. befragte Personen, Familien, Organisationen, Städte, Nachrichtensendungen, …
Variable (Merkmal)
Eigenschaft der Untersuchungseinheit
- z.B. Geschlecht, Lebenszufriedenheit, Nettoeinkommen, Alter, Arbeitslosenquote, …
Wert – Ausprägung
Merkmalsausprägung, in der eine Variable auftritt
- Geschlecht: männlich/weiblich; Lebenszufriedenheit: vollkommen zufrieden / recht zufrieden / eher unzufrieden / höchst zufrieden; Alter: Tage / Wochen / Monate / Jahre
- keine Beschränkung der Merkmalsklassen, Entscheidung liegt bei Forscher
- Werte werden häufig nach einem Codeplan codiert: sexus 1/2 (1=weiblich, 2=männlich)
Auswertung
spaltenweise – vertikal
- univariate Auswertung – 1 Spalte
- bivariate Auswertung – 2 Spalten
- multivariate Auswertung – 3-n Spalten
zeilenweise – horizontal
- mehrere Merkmale eines Merkmalträgers (meist zur Bildung von Testwerten oder neuen Merkmalen)
Beispiel:
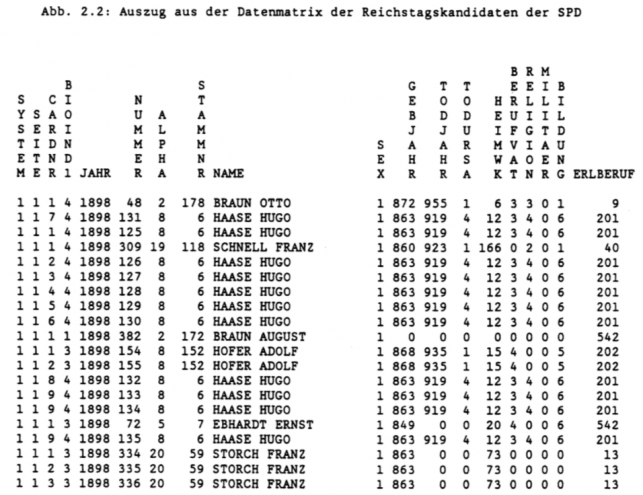
aus: Helmut Thome, Grundkurs Statistik für Historiker. Teil I: Deskriptive Statistik, HSR-TRANS 7 (2001), Version 20-12-2001,
https://www.ssoar.info/ssoar/bitstream/handle/document/28594/ssoar-hsrsupp-1989-no_2-thome-grundkurs_statistik_fur_historiker.pdf?sequence=1&isAllowed=y&lnkname=ssoar-hsrsupp-1989-no_2-thome-grundkurs_statistik_fur_historiker.pdf
Verteilungen
Werden zur Datenanalyse mehr als zwei Variablen herangezogen, spricht man von multivariaten Verteilungen, sind es genau zwei Variablen, bivariate Verteilungen und ist es nur eine Variable so handelt es sich um univariate Verteilungen.
Häufigkeitsverteilungen (frequencies)
1. Schritt der Rohdatenuntersuchung: Wie viele Untersuchungseinheiten entfallen auf eine Variablenausprägung?
Diese Zusammenstellung nennt sich Häufigkeitsverteilung (frequencies).
Es ist die Zuordnung von Variablenwerten zu der Häufigkeit ihres Vorkommens in einer Menge von Untersuchungseinheiten. Bei diskreten Variablen (best. Anzahl diskreter, deutlich voneinander getrennter Werte) kann dies problemlos erfolgen (Nominal- / Ordinalskalen), bei metrischen Daten, die einen Konitinuitätscharakter aufweisen, kann eine solche Zusammenstellung schnell unübersichtlich werden, so dass zunächst Gruppen gebildet werden müssen (gruppierte Daten), zum Beispiel: Altersangaben in Jahren können u.U. sinnvoll in 10 Jahresschritte eingeteilt werden.

aus: Helmut Thome, Grundkurs Statistik für Historiker. Teil I: Deskriptive Statistik, HSR-TRANS 7 (2001), Version 20-12-2001,
https://www.ssoar.info/ssoar/bitstream/handle/document/28594/ssoar-hsrsupp-1989-no_2-thome-grundkurs_statistik_fur_historiker.pdf?sequence=1&isAllowed=y&lnkname=ssoar-hsrsupp-1989-no_2-thome-grundkurs_statistik_fur_historiker.pdf
Graphische Darstellungen
 Übersicht über verschiedene Typen
Übersicht über verschiedene Typen
(viele verschiedene Diagrammtypen)
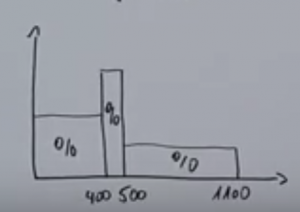
- Balkendiagramm mit und ohne Polygonzug (Häufigkeitspolygone)
Histogramme sind streng genommen nur die Balkendiagramme, die eine Klassifikation aufweisen s.u. aber sehr häufig wird der Begriff Histogramm als Synonym zu Balkendiagramm verwendet.
Diese stellen eine gebräuchliche Methode dar, um Verteilungen von kontinuierlichen Variablen zu beschreiben.
In ihrer einfachsten Form:
als Häufigkeitspolygone:
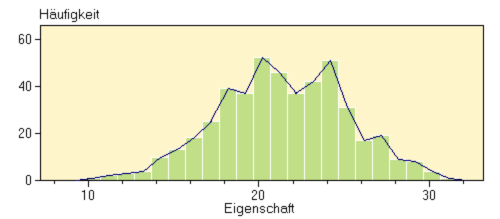
- Streifendiagramm
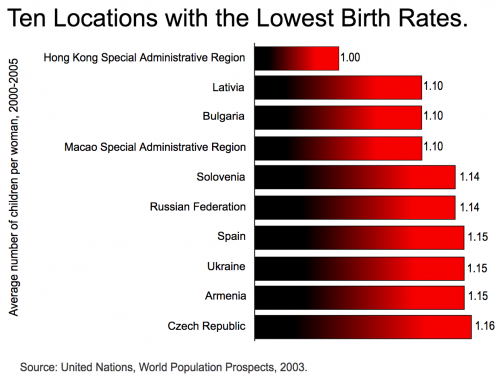
Von Ryan Cragun - de:File:Lowestbirthrates.jpg, Copyrighted free use, Link
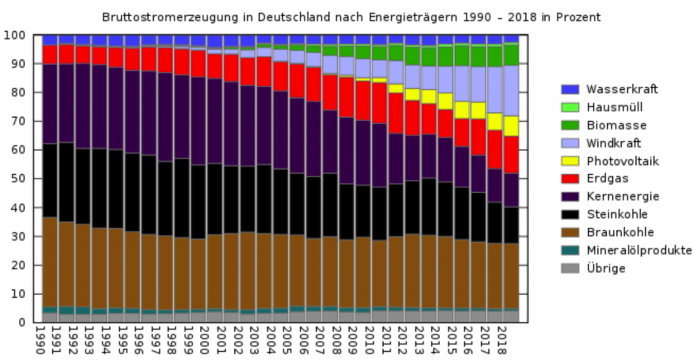
Creative Commons Attribution-Share Alike 3.0 Unported license
- Tortendiagramm
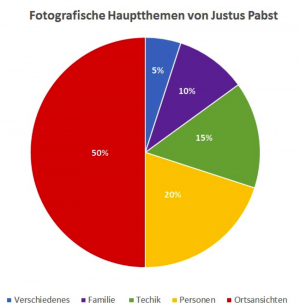
Creative Commons Attribution-Share Alike 4.0 International license
- typische Verteilungsformen
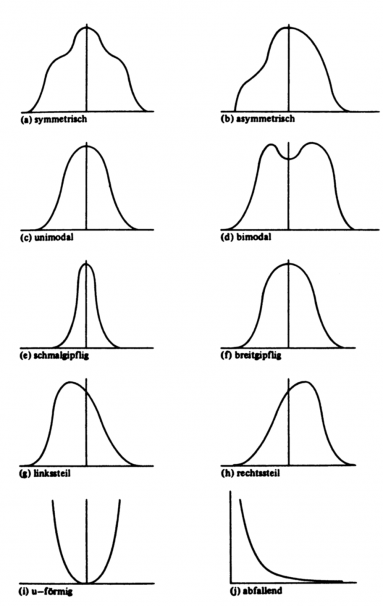
aus: Helmut Thome, Grundkurs Statistik für Historiker. Teil I: Deskriptive Statistik, HSR-TRANS 7 (2001), Version 20-12-2001,
https://www.ssoar.info/ssoar/bitstream/handle/document/28594/ssoar-hsrsupp-1989-no_2-thome-grundkurs_statistik_fur_historiker.pdf?sequence=1&isAllowed=y&lnkname=ssoar-hsrsupp-1989-no_2-thome-grundkurs_statistik_fur_historiker.pdf
Maßzahlen
Maßzahlen zur Beschreibung univariater Verteilungen - Maßzahl der zentralen Tendenz - Lagemaße
3 verschiedene Mittelwerte (Lokalisationsmaße): Mittelwert - Median - Modus
1. Modus (h) (Modalwert, mode)
- Der Wert, der häufiger vorkommt als jeder andere.
- Kann schon bei nominalen Variablen angewandt werden (am stärksten besetzte Kategorie = Modalkategorie).
2. Median ![]()
lat. medianus = in der Mitte befindlich
- es liegen ebensoviele Fälle oberhalb, wie unterhalb des Medians
- Variablen müssen mindestens Ordinalskalenniveau aufweisen
- Ausreißer finden keine/wenig Beachtung
Berechnung je nach un- oder gerader Fallanzahl (n) unterschiedlich:
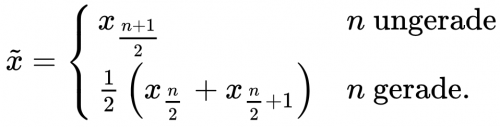
Beispiel:
11 Fälle: 3,4,4,5,6,7,8,8,8,9,10
![]() = (11 +1)/2 = 6
= (11 +1)/2 = 6
--> Wert des 6. Falles, also 7.
10 Fälle:3,4,4,5,6,7,7,8,8,9
![]() = (6+7)/2 also 6.5
= (6+7)/2 also 6.5
--> halbierte Wert der beiden in der Mitte befindlichen Werte (Unter- und Obermedian)
3. arithmetisches Mittel (mean) ![]()
- Variablen müssen metrisches Skalenniveau aufweisen
- die Summe der Meßwerte dividiert durch ihre Anzahl
- wird durch Ausreißer verzerrt
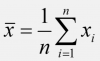
xi = Einzelner Wert der Verteilung
n = Anzahl der Werte der Verteilung
Beispiel:
10 Fälle (n):3,4,4,5,6,7,7,8,8,9
![]() = (3+4+4+5+6+7+7+8+8+9)/10 = 6,1
= (3+4+4+5+6+7+7+8+8+9)/10 = 6,1
Messniveaus / Skalentypen
3 verschiedene Skalen: Nominal, Ordinal, Intervall/Ratio/Metrische/Kardinal
Messniveaus / Skalentypen
1. Nominalskalen = niedrigstes Messniveau
- Klassifizierung
- Satz rangmäßig nicht geordneter Kategorien, mit beliebigen eindeutigen Bezeichnungen (Zahlen, Buchstaben, Wörter, geometrische Formen, ..).
- scharfe Abgrenzung der Kategorien, d.h. die Kategorien sind vollständig und schließen sich gegenseitig aus.
Beispiel:
Variable = Haarfarbe;
Variablenausprägungen:
blond = 1
braun = 2
schwarz = 3
rot = 4
Arithmetische Operationen sind bei der Verwendung von Zahlen als Kategorienbezeichnung nicht sinnvoll! Die Kennziffern für die Haarfarben fungieren als bloße Benennungen, sind Namen (= nomen, → nominal).
Meist dargestellt in Balken- oder Tortendiagrammen.
2. Ordinalskalen (Rangskalen) = niedriges-mittleres Messniveau
- Klassifizierung + Rangordnung
- Objekte können gemäß einer Eigenschaft auf einem Kontinuum angeordnet werden ( größer-kleiner-Relation)
- Die Abstände zwischen den Rangplätzen können unterschiedlich sein.
Beispiel:
Variable = Schichtenzugehörigkeit;
Variablenausprägungen:
Oberschicht = 1
Mittelschicht = 2
Unterschicht = 3
Arithmetische Operationen sind bei der Verwendung von Zahlen als Kategorienbezeichnung auch hier nicht sinnvoll!
Keine Darstellung als Tortendiaramm aber als Balkendiagramm.
3. Kardinal-, Ratio- oder Metrische Skalen (Verhältnis- oder Proportionalskalen) = höchstes Messniveau
- Klassifizierung + Rangordnung mit konstanten Abständen + invarianter Nullpunkt (metrisch)
- Skalen zum Zählen von Objekten und Ereignissen, Lebensalter, Körpergröße, -gewicht, …
Arithmetische Operationen sind hier sinnvoll:
Bei dem Vergleich einer 10 cm langen mit einer 5 cm langen Nase bin ich berechtigt festzustellen, daß die Erstere doppelt so lang ist wie die Zweite.
Darstellung als Balkendiagram, Boxplot und Liniendiagramm.
Variablentypen
Quantitative / qualitative Variablen
Objekte, die eine quantitative Merkmalsausprägung aufweisen, können hinsichtlich dieser in eine Rangfolge gebracht werden: größer oder kleiner, höher oder niedriger, mehr oder weniger.
Beispiele:
Einkommen, Alter, Lebenszufriedenheit, Religiosität, …
Objekte, die eine qualitative Merkmalsausprägung aufweisen, können hinsichtlich ihrer Art in Kategorien eingeteilt werden.
Beispiele:
Geschlecht: weiblich / männlich; Nationalität: franz., brit., deut.,andere, keine; Konfession: ev., kath., andere, keine.
Kontinuierliche / diskrete / dichotome Variablen
Quantitative Variablen sind kontinuierliche Variablen, wenn sie einen beliebigen Wert aus einem bestimmten Bereich annehmen können und keine Sprungstellen aufweisen. Sie resultieren i.A. aus einem Messvorgang.
Beispiele: Lebensalter, Körpergröße, …
Diskrete Variablen sind quantitative Variablen, die nur ganz bestimmte Werte aus einem Bereich annehmen können und Lücken und Sprungstellen aufweisen. Sie resultieren i.A. aus einem Zählvorgang.
Beispiele: Anzahl der Kinder, Einwohner, Zuschauer, …
Sonderformen der diskreten Variablen stellen die dichotomen Variablen dar, die nur zwei Merkmalsausprägungen (meist: ja/nein) aufweisen. Analog dazu gibt es trichotome (drei Merkmalsausprägungen) und polytome (mehrstufige) Variablen.
